Énoncé général du Principe Fondamental de la Dynamique
Énoncé du Principe fondamental de la Dynamique sur un solide « ponctuel »
Si le solide (S) est soumis à des actions extérieures se réduisant à une résultante \(\overrightarrow {R(ext\rightarrow S)}\) alors son mouvement est tel que :
\(\overrightarrow {R(ext\rightarrow S)} = m \times \overrightarrow {\Gamma(M /R)}\)
Somme des forces extérieures = masse du solide x vecteur accélération du point M
Unités : [N] = [kg] x [m.s-2]
Enoncé du Principe Fondamental de la Dynamique dans le cas d'un solide quelconque
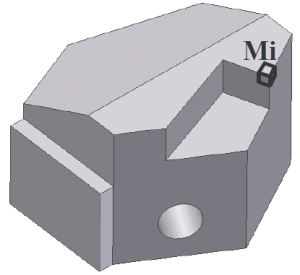
Soit un solide (S) quelconque de masse M.
Contrairement au solide précédent, celui-ci peut subir des efforts en différents points. Ceux-ci peuvent le faire tourner, il y aura donc présence de moments.
En appliquant la démonstration précédente à ce solide, il suffirait de considérer celui-ci comme la somme de points Mi, de masses mi.
Soit un solide (S) quelconque de masse m
Contrairement au solide précédent, celui-ci peut subir des efforts en différents points. Ceux-ci peuvent le faire tourner, il y aura donc présence de moments.
En appliquant la démonstration précédente à ce solide, il suffirait de considérer celui-ci comme la somme de points Mi, de masses mi.
Si le solide (S) est soumis à des actions mécaniques extérieures quelconques :
\(\{\mathcal{T}(ext \rightarrow S) \} = \begin{array} {c}\\ \\\\\end{array} _A {\left\{ \begin{array} {cc} \overrightarrow {R_{(ext\rightarrow S)}} \\ \overrightarrow {M_{A,(ext\rightarrow S)}} \\\end{array} \right\} }_{{(\vec{x},\vec{y},\vec{z})}}\)
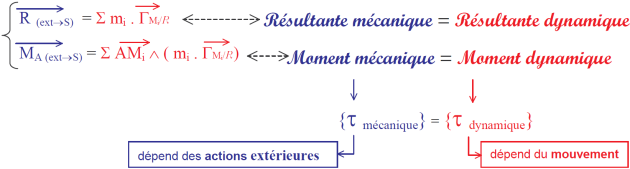
Alors son mouvement dans un repère Galiléen est tel que, quel que soit A :
Remarque :
Pour ce qui est du torseur mécanique (à gauche), ceci a été déjà vu dans les séquences précédentes : c'est un bilan des actions extérieures.
Le torseur dynamique contient en revanche des relations inutilisables telles quelles pour un élève de terminale, mais nous allons dans la suite nous intéresser aux cas particuliers de la translation et de la rotation autour d'un axe fixe.
Vous noterez également que le Principe Fondamental de la Statique n'est qu'un cas particulier du PFD, à accélération nulle, c'est à dire pour un corps immobile ou en translation rectiligne uniforme dans un repère galiléen (le "torseur dynamique" est nul).
Théorème de la résultante
On peut montrer que dans tous les cas :
\(\Sigma m_i \times \overrightarrow {\Gamma(M_i/R)} = M \times \overrightarrow {\Gamma(G/R)}\)
\(M \)est la masse totale et \(\overrightarrow {\Gamma(G/R)}\) le vecteur accélération du centre de gravité G.
Ce qui donne : \(\overrightarrow {R(ext\rightarrow S)} = M \times \overrightarrow {\Gamma(G/R)}\) quels que soient le solide et son mouvement.
Ce théorème permet déjà d'utiliser facilement le PFD dans le cas d'une translation.