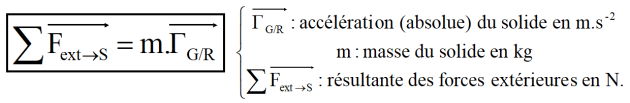Principe Fondamental de la Dynamique : cas d'une translation rectiligne
Fondamental : Théorème de la résultante
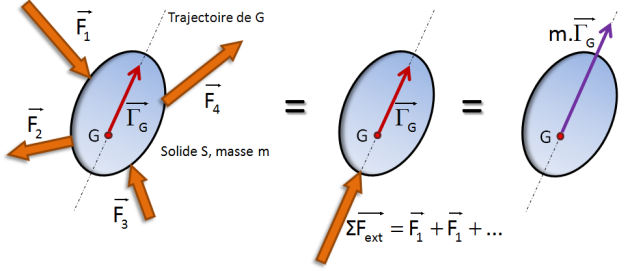
On peut montrer que dans tous les cas :
\(\Sigma m_i \times \overrightarrow {\Gamma(M_i/R)} = M \times \overrightarrow {\Gamma(G/R)}\)
\(M \)est la masse totale et \(\overrightarrow {\Gamma(G/R)}\) le vecteur accélération du centre de gravité G.
Ce qui donne : \(\overrightarrow {R(ext\rightarrow S)} = M \times \overrightarrow {\Gamma(G/R)}\) quels que soient le solide et son mouvement.
Ce théorème permet déjà d'utiliser facilement le PFD dans le cas d'une translation.
L'énoncé proposé s'applique indifféremment à un point matériel de masse m ou à un solide en translation rectiligne de masse m et centre de gravité G.
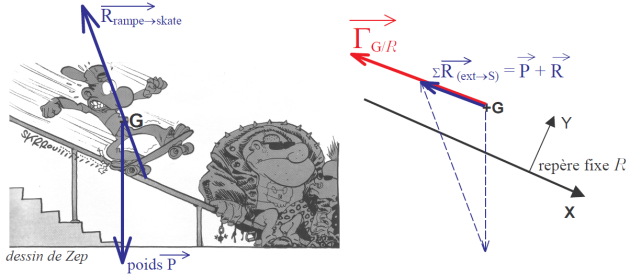
L'accélération \(\overrightarrow {\Gamma_{(G/R)}}\) (ou \(\overrightarrow {a_{(G/R)}}\) ) du centre de gravité G du solide en translation rectiligne par rapport à un repère (ou solide) absolue est proportionnelle à la résultante (\(\overrightarrow {R_{(ext \rightarrow S)}}=\Sigma \overrightarrow {F_{(ext \rightarrow S)}}\) ) des forces ou actions extérieures agissant sur le solide et a même direction et même sens que celle-ci.
Exemple : Autre exemple
