L'inertie en mouvement de rotation
Exemple : Exemple permettant de dissocier masse et inertie en mouvement de rotation
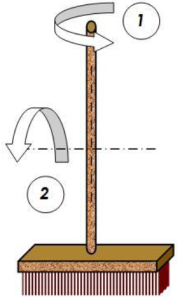
Le manche à balais étant initialement à l'arrêt.
Quel est le cas qui nécessite un couple plus important pour mettre la balais en mouvement de rotation ?
Lorsque l'on prend un balai en main au milieu du manche et qu'on le fait tourner comme sur la figure ci-contre, il est plus aisé de le faire tourner autour de l'axe du manche (1), qu'autour de l'axe transversal indiqué (2).
Cela est dû au fait que dans le deuxième cas, la matière constituant le balai se trouve plus éloignée de l'axe de rotation. Comme pour un solide en rotation, la vitesse linéaire d'un point croît en proportion avec cet éloignement, il est nécessaire de communiquer une plus grande énergie cinétique aux points éloignés. D'où la plus grande résistance du balai à tourner autour d'un axe transversal qu'autour de l'axe du manche.
Exemple :
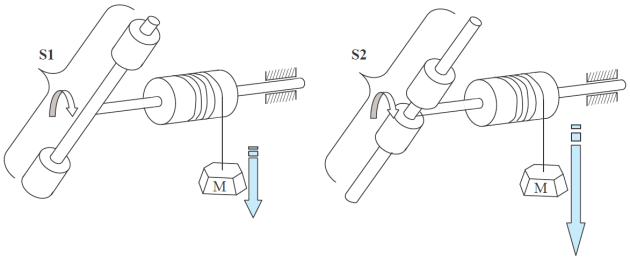
Les deux objets ci-dessous sont identiques, hormis la position des masselottes qui est plus éloignée du centre de rotation pour le solide S1.
On lâche les masses M simultanément.
Constatation :
La masse liée au solide S2 descend plus vite. Le solide S2 est plus facile à mettre en mouvement de rotation que S1.
Les deux solides ont pourtant la même masse mais répartie différemment par rapport à l'axe de rotation.
Ils n'ont pas le même moment d'inertie.
Définition : Inertie
L'inertie quantifie pour un corps la masse et son éloignement par rapport à l'axe de rotation.
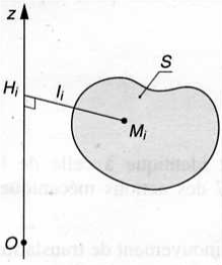
En théorie, on détermine l'inertie en effectuant\( J_{(O, \vec z})=\int l_i ^2 dm\): la somme (en intégrant) pour chaque point Mi le produit de sa masse et de sa distance par rapport à l'axe au carré.
Dans la pratique on utilise des formulaires et des données constructeurs (Cf. Calcul du moment d'inertie).
Remarque : unité de l'inertie J : kg.m2