Modéliser le mouvement d'un point appartenant à un solide en translation
La modélisation du mouvement d'un solide se traduit par 3 équations horaires générales du mouvement selon la définition de l'accélération (nulle, constante ou variable). Les équations qui suivent, ne s'appliquent pas pour une accélération variable (dans ce cas, il faudra utiliser un logiciel de simulation).
Fondamental : Mouvement de Translation Uniforme :Accélération nulle : a(t) = 0
Équations horaires générales du mouvement uniforme (MU) :
a(t) = 0
v(t) = constante = vi
x(t) = vi . ( t - ti ) + xi
où xi, vi et pi sont les conditions initiales (ce sont des constantes à déterminer).
Exemples d'applications et allures des courbes caractéristiques des équations horaires :
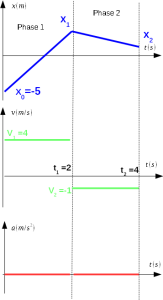
Exemple phase1 : trouver x1 connaissant v1 et t1
x1 = v1 (t1-t0) + x0
= 4 (2-0) + (-5) = 3 m
Exemple phase 2 : trouver v2 connaissant x2 et t2
x2 = v2(t2-t1) +x1
\(v2 = \frac {x_2 - x_1} {t_2 - t_1} = \frac {1-3} {4 - 2} = -1 m/s\)
Fondamental : Mouvement de Translation Uniformément Varié : Accélération constante : a(t) = constante
Équations horaires générales du mouvement uniformément varié (MUV) :
a(t) = constante = ai
v(t) = ai . ( t - ti ) + vi
x(t) = 0,5 . ai . ( t - ti )2 + vi . ( t - ti ) + xi
où ti, ai, vi et pi sont les conditions initiales (ce sont des constantes à déterminer).
Exemples d'applications et allures des courbes caractéristiques des équations horaires :
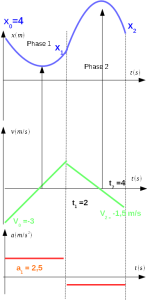
Exemple phase1 : trouver x1 et v1 connaissant a1,v0 et t1
\(x_1= \frac {1} {2} a_1 (t_1-t_0) ^2 + v_0(t_1-t_0) + x_0 =\)
\(x_1= \frac {1} {2} 2.5 (2-0) ^2 -3(2-0) + 4 = 3 m\)
v1 = a(t1-t0) + v0
v1 = 2.5 (2-0) -3 = 2 m/s
Exemple phase 2 : trouver et a2 et x2 connaissant v2 et t2
v2 = a2(t2-t1) +v1
\(a2 = \frac {v_2 - v_1} {t_2 - t_1} = \frac {-1.5-2} {4 - 2} = -1.75 m/s2\)
\(x_2= \frac {1} {2} a_2 (t_2-t_1) ^2 + v_1(t_2-t_1) + x_1 =\)
\(x_2= \frac {1} {2}(- 1.5) (4-2) ^2 + 2(4-2) + 2 =3m\)
Remarque :
La distance d parcourue pendant une phase de mouvement correspond à la différence de positions entre le début et la fin de la phase :
d = xf -xi