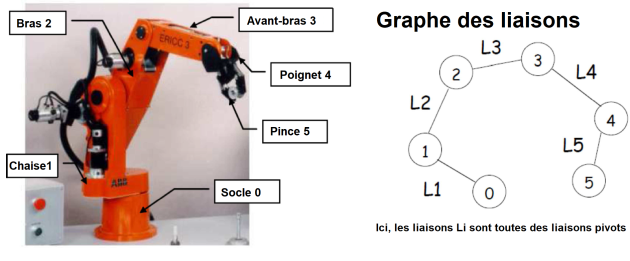
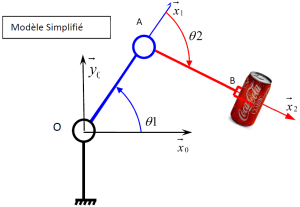
Exemple dans le cas d'une chaîne cinématique ouverte
Dans le cas des chaînes cinématiques ouvertes, la loi E/S concerne la relation entre les coordonnées articulaires et les coordonnées opérationnelles du point en bout de chaîne. A cet effet on établit un modèle géométrique indirect à partir d'une relation de Chasles
Exemple : Bras de robot
On considère le modèle plan simplifié dans lequel la pince de robot n'est animé que par deux mouvements de rotation paramétré \(\theta_1\) et \(\theta_2\). Chaque bras du robot est de longueur L.
Le point B en bout de chaîne a comme coordonnée \(x_B\) et \(y_B\) dans repère \(\mathfrak{R}_{0}(O,\vec{x_0},\vec{y_0},\vec{z_0})\).
Le modèle géométrique direct permet d'exprimer les coordonnées \(x_B\) et \(y_B\) en fonction des paramètres \(\theta_1\) et \(\theta_2\).
En écrivant la relation de Chasles \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=L.\vec{x_1}+L.\vec{x_2}\).
Avec \(\vec{x_1}=\cos\theta_1.\vec{x_0}+\sin\theta_1.\vec{y_0}\) et \(\vec{x_2}=\cos(\theta_1+\theta_2).\vec{x_0}+\sin(\theta_1+\theta_2).\vec{y_0}\)
On a donc, \(\overrightarrow{OB}=[L.\cos\theta_1+L.\cos(\theta_1+\theta_2)].\vec{x_0}+[L.\sin\theta_1+L.\sin(\theta_1+\theta_2)].\vec{y_0}\).
Après projection dans le repère \(\mathfrak{R}_{0}\), on arrive à déterminer le modèle géométrique direct :
\(\Biggl\{\begin{matrix} x_B=L.\cos\theta_1+L.\cos(\theta_1+\theta_2) \\ y_B=L.\sin\theta_1+L.\sin(\theta_1+\theta_2) \end{matrix}\)
Remarque : Relation indirecte
Le modèle géométrique indirect permet d'exprimer les paramètres \(\theta_1\) et \(\theta_2\) en fonction des coordonnées \(x_B\) et \(y_B\).
Le modèle géométrique indirect est plus délicat à trouver il faut utiliser :
La transformation de somme trigonométrique en produit
Utiliser\( x_B²+y_B²\) (Pythagore) puis \(\frac{y_B}{x_B}\)
On détermine ainsi le modèle géométrique indirect (ici hauteur a = 0) :
\(\Biggl\{\begin{matrix} \theta_2=\arccos \left[ \frac{1}{2}.\left( \left( \frac{x_B}{L}\right)^2+\left( \frac{y_B}{L}\right)^2 \right)-1\right] \\ \theta_1=\left(\arctan \frac{y_B}{x_B}\right)-\frac{\theta_2}{2}\end{matrix}\)