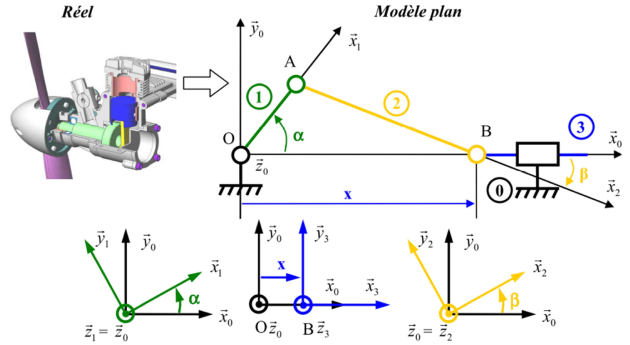
Exemple dans le cas d'une chaîne cinématique fermée
La loi E/S dans les chaînes cinématiques fermées peut être obtenue de différentes méthodes :
fermeture géométrique ou fermeture angulaire,
produit scalaire de 2 vecteurs d'orientation relative constante,
l'équation obtenue par la condition de roulement sans glissement,
la fermeture cinématique.
Dans le cadre de l'enseignement de spécialité, on se contentera de la méthode de la fermeture géométrique.
Loi entrée /sortie par fermeture géométrique
La loi entrée / sortie dans le cas de chaîne fermée s'obtient souvent par fermeture géométrique. Il s'agit d'écrire une relation vectorielle (relation de Chasles), traduisant la fermeture de la chaîne, en passant par les points caractéristiques du mécanisme. On projette ensuite cette relation dans une base (choisi judicieusement pour limiter les calculs) afin d'obtenir des relations scalaires entre les différents paramètres, puis on élimine les paramètres intermédiaires afin d'établir notre relation entre le paramètre d'entrée et le paramètre de sortie du mécanisme.
Exemple : Système bielle manivelle
Transformation : Rotation continue en translation alternative et inversement si système réversible,
Utilisation : Moteurs thermiques ou hydrauliques, compresseurs, certaines pompes, marteau perforateur...
Caractéristiques : excentricité OA = L1 longueur de la manivelle 1 et AB = L2 longueur de la bielle 2.
Le paramètre d'entrée dépend du mode d'utilisation du système bielle manivelle :
utilisé comme moteur, Le paramètre d'entrée est \(x\) représentant la translation du piston ;
utilisé comme compresseur, le paramètre d'entrée est \(\alpha\) représentant la rotation de la manivelle ou vilebrequin.
Pour ce micromoteur, le paramètre d'entrée est donc \(E = x\) (translation du piston), et le paramètre de sortie est \(S = \alpha\) (rotation de la manivelle ou vilebrequin).
Le paramètre \(\beta\) est un paramètre intermédiaire traduisant la position angulaire de la bielle par rapport au bâti.
On écrit la fermeture géométrique :
\(\overrightarrow{OO}=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{BO}=L_1.\vec{x_1}+L_2.\vec{x_2}-x.\vec{x_0}\).
En projection sur \(\vec{x_0}\) et \(\vec{y_0}\), on obtient deux équations scalaires :
\(\Biggl\{\begin{matrix} L_1.\cos\alpha+L_2.\cos\beta-x=0 \\ L_1.\sin\alpha+L_2.\sin\beta=0 \end{matrix}\)
Afin d'obtenir la loi entrée/sortie on élimine le paramètre \(\beta\) en élevant au carré chacune des relations et en les additionnant.
\(\Biggl\{\begin{matrix} \cos\beta=\frac{x-L_1.\cos\alpha}{L_2} \\ \sin\beta=-\frac{L_1.\sin\alpha}{L_2} \end{matrix}\) et comme \(\cos² \beta+\sin² \beta=1\)
Ce qui donne : \(\left(\frac{x-L_1.\cos\alpha}{L_2}\right)^2+\left(-\frac{L_1.\sin\alpha}{L_2}\right)^2=1\)
D'où : \(\left(x-L_1.\cos\alpha\right)^2=L_2^2-\left(L_1.\sin\alpha\right)^2\)
Soit la loi entrée-sortie : \(x=L_1.\cos\alpha+\sqrt{L_2^2-\left(L_1.\sin\alpha\right)^2}\).
Cette relation est valable seulement pour \(L_1 < L_2\).