Control'X

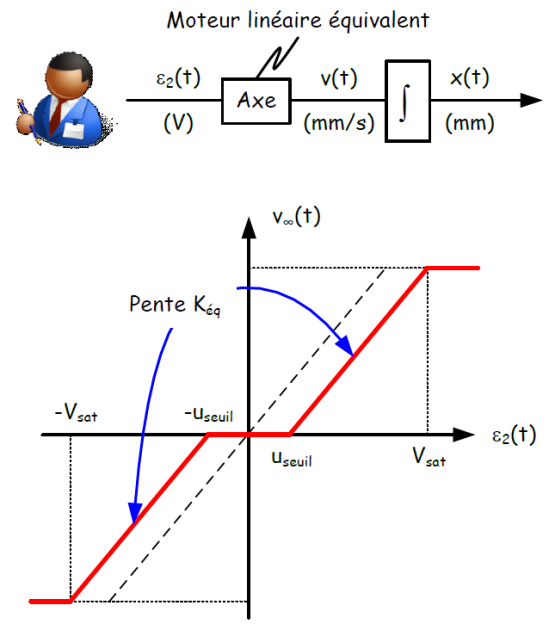
Moteur sans dynamique : Pour une tension d'alimentation constante donnée \(\varepsilon_2(t)\), la vitesse V_∞(t) est atteinte immédiatement. Tension de seuil u_seuil négligée. Tension de saturation Vsat prise en compte.

Moteur sans dynamique. Tension de seuil u_seuil et tension de saturation V_sat prises en compte.

Dynamique du moteur prise en compte : Système caractérisé par une équation différentielle du premier ordre du type : \(\tau_{eq}.\dfrac{dv(t)}{dt}+v(t)=K_{eq}.\varepsilon_2(t)\).

Tension de seuil u_seuil et tension de saturation V_sat prises en compte.

Montrer que dans le cas du modèle 2 (le modèle 1 se déduit du modèle 2), la position obtenue (CI nulle) correspond à l'intégrale de la tension d'alimentation \(\varepsilon_2(t)\) appliquée :

\(x(t)=K_{eq}. \displaystyle \int_{\lambda=0}^{\lambda=t} [\varepsilon_2(\lambda)-u_{seuil}] \, \mathrm{d}\lambda\) si \(\varepsilon_2(t) \in[-V_{sat}, V_{sat}]\).

On cherche maintenant à piloter le système, toujours en boucle ouverte, mais en imposant un signal \(\varepsilon_2(t)\) calculé (programmé) de façon à ce que le chariot se positionne à 300 mm. Exploiter les modèles 1 et 2 pour calculer la durée pendant laquelle il est nécessaire d'appliquer la tension constante \(\varepsilon_2(t)\) pour que le chariot se positionne à 300 mm.