Collectif 2 : Performances du positionnement
Que se passe-t-il si le modèle ne reflète pas correctement la réalité ou si les valeurs numériques du modèle sont mal choisies ?
Pourrait-on calculer l'évolution de la tension \(\varepsilon_2(t)\) à appliquer compte tenu des perturbations qui par définition sont non prévisibles ?
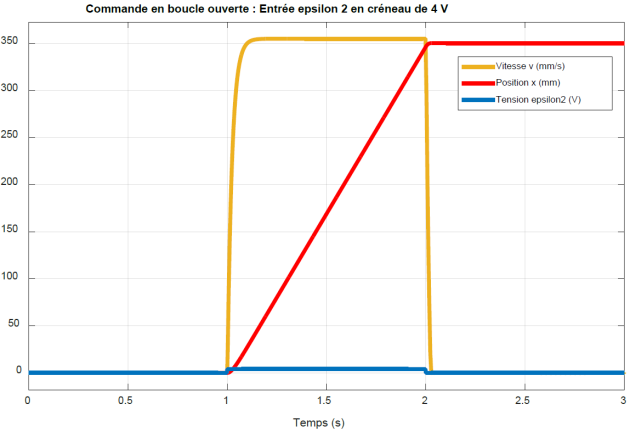
La dynamique de mise en mouvement du moteur a été négligée. Cela a-t-il une grosse influence sur la distance parcourue. Interpréter physiquement pour cela les courbes ci-dessous : la distance parcourue (courbe rouge) est l'aire sous tendue par la courbe de vitesse (courbe jaune).
Les constats précédents nous amènent à imaginer un mode de commande de l'axe de type automatique. Un mode de commande où le pilotage se ferait non plus en imposant en entrée une commande en volts mais directement la position souhaitée en mm (la consigne), le système calculant lui-même la tension \(\varepsilon_2(t\)) à appliquer pour aller au but dans les meilleures conditions.
Un tel système s'appelle un système asservi : du latin "servus", l'esclave. C'est un système dont la sortie (l'esclave) est censée suivre la consigne (le maître) en toutes circonstances.
Le but étant de positionner le chariot le plus rapidement possible, le plus précisément possible et ce malgré la présence d'éventuelles perturbations. La cerise sur le gâteau serait que les performances de positionnement n'aient pas (ou peu) à dépendre de :
la finesse d'un quelconque modèle mis en place. C'était loin d'être le cas jusqu'à présent.
la modification éventuelle au cours du temps de certains paramètres caractéristiques du système (frottements dans le mécanisme par exemple)