Collectif 3 : Bilan des observations
Faire le point sur les comportements observés avec les différentes stratégies de pilotage mises en place.
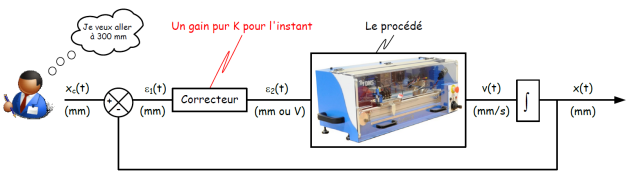
La stratégie la plus utilisée (dans le domaine de la commande d'axe notamment) lorsque l'on souhaite obtenir des performances de premier plan consiste à utiliser une structure de boucle fermée reposant sur un soustracteur suivi d'un correcteur.
Le correcteur que nous avons utilisé est un correcteur proportionnel : pour élaborer la tension de commande ε2(t), il multiplie l'écart ε1(t) en sortie de soustracteur par un facteur constant K.
Il existe une multitude d'autres types de correcteurs, certains permettent de tenir compte de tous les écarts passés et de l'écart futur estimé.
Le correcteur voit : c'est lui qui observe l'écart ε1(t) entre ce qui est souhaité et ce qui est réellement obtenu.
Le correcteur pense : c'est le cerveau de l'asservissement, c'est lui qui prend les décisions.
Le correcteur parle : c'est lui qui génère la commande \(\varepsilon_2(t)\) à destination du procédé.
... Mais le correcteur ment, il dramatise : le coefficient K permet de tricher pour "faire croire" au procédé que l'écart n'est pas ce qu'il est réellement.
Grâce au coefficient K, le correcteur "fait croire" au procédé que l'écart ne vaut pas \(\varepsilon_1(t)\) mais \(ε2(t) = K.ε1(t)\). Si K = 5 par exemple, il "fait croire" au procédé que l'on est 5 fois plus loin du but à atteindre qu'on ne l'est réellement.
On travaille maintenant dans l'onglet "Analyse temporelle" de Control'Drive. Réinitialiser le chariot et imposer un gain de correcteur de 0.05 (Menu "Correcteur"). Imposer une consigne en échelon de 300 mm d'amplitude : menu "Analyse temporelle", "Définir entrée", onglet "Echelon" puis cliquer sur "Lancer mouvement". Observer le positionnement de façon très qualitative.
Modifier le gain du correcteur que l'on prendra parmi {0.1, 1, 2, 5, 10} et, après avoir réinitialisé la position du chariot (bouton rouge "Réinitialiser"), lancer de nouveaux échelons. Une fois le chariot stabilisé, exercer y des perturbations à la main. Observez le comportement du système.
Il faut remarquer qu'en boucle fermée, à aucun moment, il n'a été nécessaire de faire de la modélisation pour pouvoir asservir la position du chariot. Les performances du positionnement sont par contre affectées par le choix du correcteur et ce correcteur ne se choisit en général pas au hasard. Ce n'est pas la modélisation qui permet d'asservir mais la modélisation par contre va être nécessaire voire indispensable pour nous permettre de choisir un correcteur qui optimise les performances de l'asservissement.
Conseil : S'il vous reste du temps
Analyser et tenter de comprendre la façon dont la position du chariot est technologiquement mesurée avant d'être soustraite à la consigne.
Complément :
Pour conclure, on cite ici quelques explications extraites d'un cours de commande robuste de Pierre Apkarian, chercheur à l'ONERA :
Rappelons qu’un asservissement a deux fonctions essentielles :
Façonner la réponse du système asservi pour lui imprimer le comportement désiré
Maintenir ce comportement face aux aléas et fluctuations qui affectent le système pendant son fonctionnement (rafales de vent pour un avion, usure pour un système mécanique, changement de configuration pour un robot, etc.).
Cette seconde exigence est qualifiée de “robustesse à l’incertitude”. Elle revêt une importance critique pour la fiabilité du système asservi. En effet, l’asservissement est typiquement conçu à partir d’un modèle idéalisé et simplifié du système réel. Pour fonctionner correctement, il doit donc être robuste :
aux imperfections du modèle, c’est-à-dire aux écarts entre le modèle et le système réel
aux dérives des paramètres physiques
aux perturbations externes.