Programmation
La structure de programmation est identique a celle de tous les langages.
Toute ligne précédée du symbole # est considérée comme un commentaire.
R n'est pas sensible a l'indentation, par contre il est sensible a la casse R<-2 et r<-3 sont deux variables différentes.
Si . . .alors . . .sinon
Exemple : maximum de deux nombres
1
a<-12
2
b<-15
3
if(a<b)(M<-b) else (M<-a)
4
print(M)
5
# on peut crer une fonction et utiliser ifelse6
Max<-function(a,b)
7
{8
ifelse(a<b,M<-b,M<-a)
9
return(M)
10
}
11
# pour appeler la fonction12
Max(a=12,b=15)
La boucle « pour »
1
somme des 10 premiers entiers naturels
2
S<-0
3
for(i in 1:10){S<-S+i}
4
print(S)
la boucle « tant que »
Le pgcd de deux entiers naturels
1
pgcd<-function(a,b)
2
{3
c<-a
4
d<-b
5
# si a est rel il sera transformeen entier par as.integer#6
a<-as.integer(a)
7
b<-as.integer(b)
8
while(a!=b) # les deux symboles "!=" signifie non egle
9
{10
if (a>b) {a<-a-b}else{b<-b-a}
11
}
12
res<-paste("le PGCD de ",c,"et",d,"est",a)
13
print(res)
14
}
La récursivité : suite de Fibonacci
1
fibo<-function(n){
2
if (n==0)(result<-1)
3
else{if (n==1)(result<-1) else {result<-fibo(n-1)+fibo(n-2)}}
4
return(result)
5
}
6
# afficher les dix premiers termes de la suite7
suite<-NULL
8
for(i in 1:10)(suite[i]<-(fibo(i)))
9
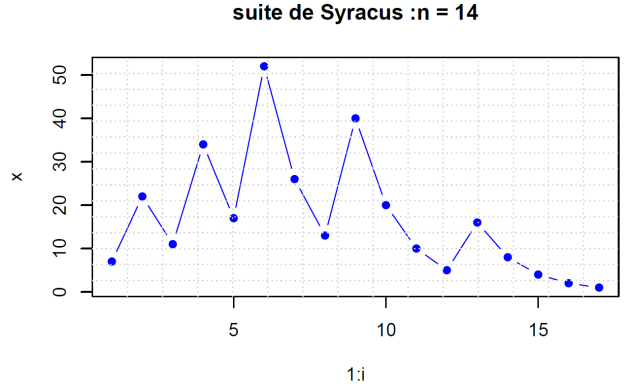
suiteCalcul et représentation des premiers éléments de la suite de Syracus
1
n<-14
2
i<-0
3
x<-NULL
4
s<-n
5
while(s>1)
6
{7
ifelse(s%%2==0, s<-s/2,s<-3*s+1)
8
i<-i+1
9
x[i]<-s
10
}
11
temps_vol<-length(x)
12
altitude<-max(x)
13
abscisse<-which(x==altitude)
14
temps_vol1
altitude1
abscisse