Statistique a deux variables
On se limite au cas ou il existe deux variables représentées par deux vecteurs sans effectifs. Généralement il existe une variable
explicative x, \(t\), ... et une variable à expliquer \(y\), \(z\), ... , il faut bien distinguer les deux variables. Etudions l'exemple suivant, en commençant par le nuage de points.
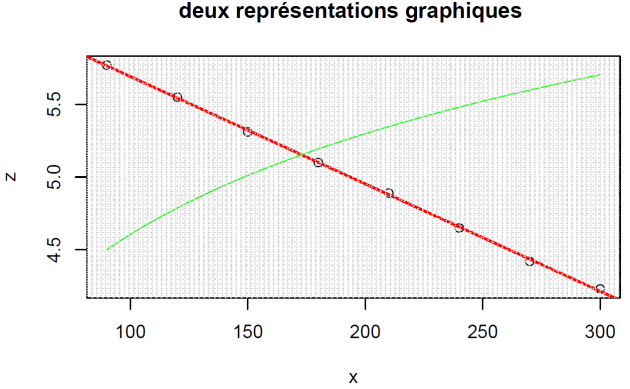
Nuage de points
x<-c(90 ,120,150,180,210,240, 270,300 )
z<-c(5.77, 5.55, 5.31, 5.10 ,4.89 ,4.65, 4.42, 4.23)
plot(x,z,main="nuage de pts de z en fonction de x")
Coefficient de corrélation
x<-c(90 ,120,150,180,210,240, 270,300 )
z<-c(5.77, 5.55, 5.31, 5.10 ,4.89 ,4.65, 4.42, 4.23)
r<-cor(x,z)
Droite de régression
C'est le modèle linéaire qui est utilise par R-Project (Linear Model ou lm), basée sur la méthode des moindres carres.
resultat<-lm(z~x)
resultatNous avons crée une variable résultat qui contient tous les résultats réalisés par notre modèle.
On s'aperçoit que l'exécution de cette fonction donne les deux coefficients de la droite de régression : une valeur est affichée sous Intercept (elle correspond à l'ordonnée à l'origine) et une valeur sous la lettre \(x\) qui correspond au coefficient directeur de la droite de regréssion.
Remarque :
Les équations de droite sont généralement notées : \(y = a+bx\), d'ou l'origine de la fonction abline. Pour tracer, avec R, la droite d'equation \(y = 2x + 1 = 1 + 2x\), il suffit de saisir abline(a=1,b=2) ou tout simplement abline(1,2).
La pente et l'ordonnée a l'origine
On peut isoler les paramètres de la droite de régression de la manière suivante :
resultat<-lm(z~x)
ord<- resultat$coefficients[1]
pente<-resultat$coefficients[2]
Tracé de la droite de régression
Pour tracer la droite de régression, il faut reprendre le programme de départ et le compléter par abline comme ceci :
x<-c(90 ,120,150,180,210,240, 270,300 )
z<-c(5.77, 5.55, 5.31, 5.10 ,4.89 ,4.65, 4.42, 4.23)
plot(x,z,main="nuage de pts de z en fonction de x")
abline(resultat)
grid(20)
Ajout d'une courbe dans un graphique existant ( avec add=TRUE ou add =T)
Remarque :
Les réels 90 et 300 sont les bornes de l'intervalle dans lequel la fonction doit être étudiée.
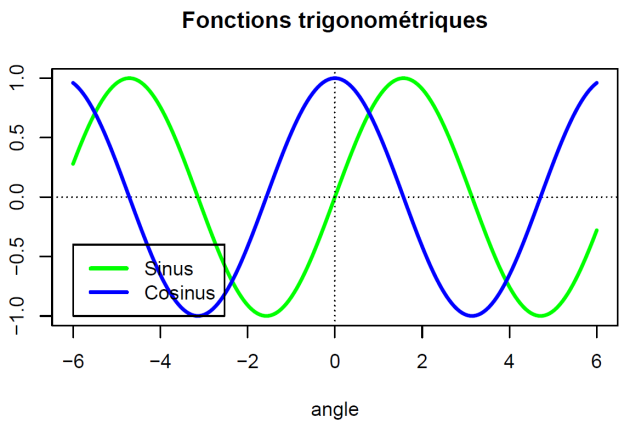
Ajout d'une légende a un dessin avec la fonction legend
x <- seq(-6,6,length=200)
y <- sin(x)
z <- cos(x)
plot(y~x, type='l', lwd=3,
ylab='', xlab='angle', main="Fonctions trigonomtriques",col='green')
abline(h=0,lty=3)
abline(v=0,lty=3)
lines(z~x, type='l', lwd=3, col='blue')
legend(-6,-1, yjust=0,c("Sinus", "Cosinus"),lwd=3, lty=1, col=c('green', 'blue'))
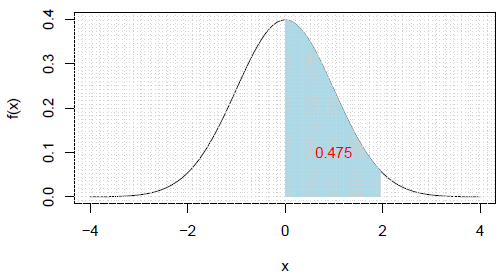
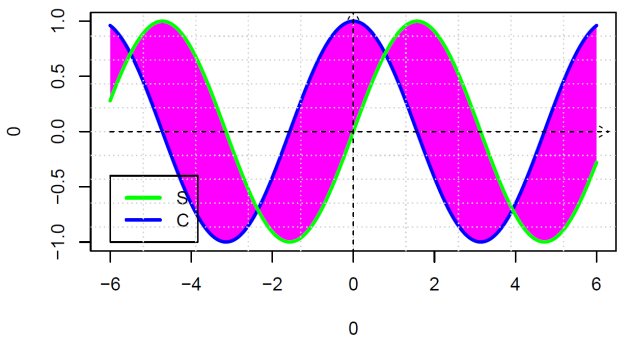
On peut colorier des parties du dessin a l'aide de la commande polygon
ColorDessin <- function (f, g, xmin, xmax, col, N=200) {
x <- seq(xmin,xmax,length=N)
fx <- f(x)
gx <- g(x)
plot(0,0, type='n',
xlim=c(xmin,xmax),
ylim=c( min(fx,gx), max(fx,gx) ) )
polygon( c(x,rev(x)), c(fx,rev(gx)), col=rgb(1,0,1), border=0 )
lines(x,fx,lwd=3,col='blue')
lines(x,gx,lwd=3,col='green')
}
ColorDessin( function(x) cos(x), function(x) sin(x), -6, 6)
legend(-6,-1, yjust=0,c("S", "C"),lwd=3, lty=1, col=c('green', 'blue'))
grid(10)
arrows(-6,0,6.3,0,length = 0.1,lty='dashed')
arrows(0,-6,0,1.1,length = 0.1,lty='dashed')
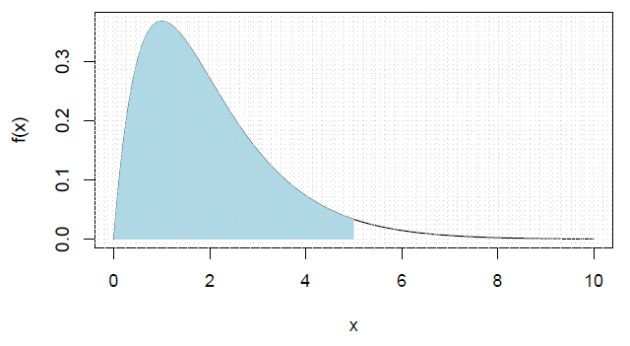
Hachurer un domaine plan en vue de calculer son aire
domaine<- function (f, xmin, xmax,a,b, col, N=200) {
N<-200
curve(f(x),xmin,xmax)
intervalle <-seq(a,b,l=N)
fx <- f(intervalle)
gx <- rep(0,N)
polygon( c(intervalle,rev(intervalle)), c(fx,rev(gx)), col='light blue', border=0 )
grid(50)
}
domaine(function(x) x*exp(-x), 0, 10,a=0,b=5)