La Méthode de Monte Carlo : MMC
La méthode de Monte-Carlo est une méthode probabiliste permettant le calcul approche d'intégrales (simples ou multiples) de fonctions quelle que soit leur régularité. C'est cette propriété qui explique son intérêt par rapport aux méthodes déterministes classiques.
Pour simplifier cette présentation, on suppose que l'on cherche a calculer : \(p=\displaystyle\int_0^1 f(t) \, dt\) pour une fonction continue dur [0 ;1] à valeurs dans [0 ;1].
Il existe deux méthodes
Méthode dite du 'rejet'
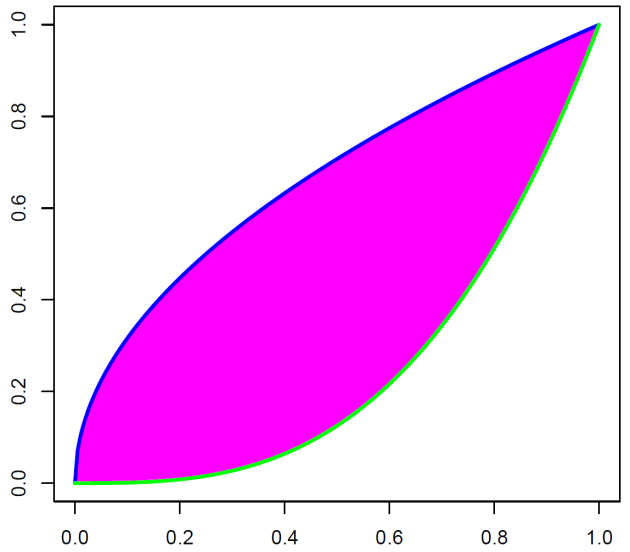
Rappelons que p est l'aire du domaine : \(D = {(x; y) \in [0; 1]^2 \quad y \leq f(x) }\)
Une première méthode possible est de tirer aléatoirement un grand nombre de points du carre \([0; 1]^2\) et de faire le quotient entre le nombre de points situés dans le domaine \(D\) et le nombre total de points.
Calcul de \(\displaystyle\int_0^1 e^{-x^2} \, dx\) par la méthode du rejet
nbsimul<-1000; compteur<-0
for (i in 1:nbsimul)
{x<-runif(1); y<-runif(1)
if (y<exp(-x^2))(compteur<-sum(compteur,1))
}
aire<-compteur/nbsimul
aireMéthode d'espérance
On admet le résultat suivant :
Si \(X\) est une variable aléatoire suivant une loi uniforme sur [0,1] et si \(f\) est une fonction continue sur [0,1] alors la variable aléatoire \(Y = f(X)\) possède une espérance égale à \(p=\displaystyle\int_0^1 f(t) \, dt\)
Calcul de \(\displaystyle\int_0^1 e^{-x^2} \, dx\) par la méthode d'espérance
nbsimul<-1000; y<-NULL
for (i in 1:nbsimul){x<-runif(1);y[i]<-exp(-x^2)}
aire<-sum(y)/nbsimul
aireExercice
Rejet
nbsimul<-1000; compteur<-0
for (i in 1:nbsimul)
{x<-runif(1); y<-runif(1)
if (y<sqrt(x)&&y>x^3)(compteur<-sum(compteur,1))
}
aire<-compteur/nbsimul
aireb_inf<-aire-1.96*sqrt(aire*(1-aire))/sqrt(nbsimul)
b_sup<-aire+1.96*sqrt(aire*(1-aire))/sqrt(nbsimul)
print ('intervalle de confiance 95%')
cat(paste('[',round(b_inf,3),',',round(b_sup,3),']'))
Espérance
nbsimul<-1000; y<-NULL
for (i in 1:nbsimul){x<-runif(1);y[i]<-sqrt(x)-x^3}
aire<-sum(y)/nbsimul
aireb_inf<-aire-1.96*sqrt(aire*(1-aire))/sqrt(nbsimul)
b_sup<-aire+1.96*sqrt(aire*(1-aire))/sqrt(nbsimul)
print ('intervalle de confiance 95%')
at(paste('[',round(b_inf,3),',',round(b_sup,3),']'))
Autre version
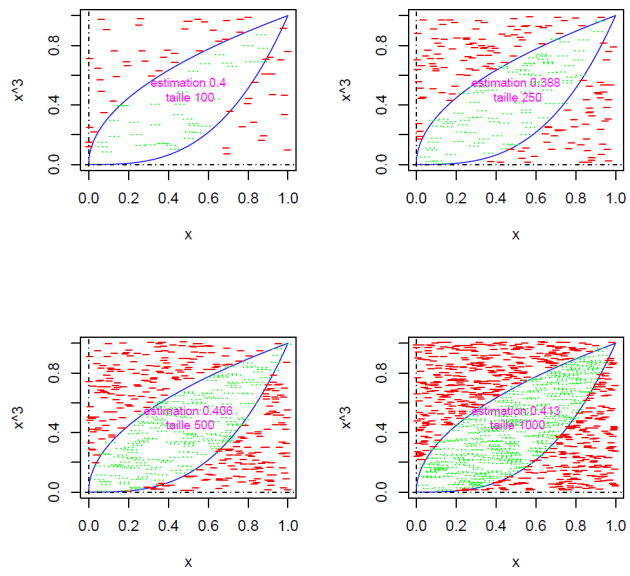
par(mfrow=c(2,2))# quatre figure dans une fen^etre
#-------------------------------- Fonction Mont Carlo-------------------------------#MonteCarlo<-function(nbsimul=100){
curve(x^3, 0,1,n=1000,col='blue')# bordure basse de la feuille
curve(sqrt(x),0,1,1000,col='blue',add=T)# bordure haute
abline(h=0,v=0,lty=4)# les axes du repee
compteur<-NULL
for (i in 1:nbsimul){
x<-runif(1)# tirage d'un nombre aleaoire entre 0 et 1
y<-runif(1)
if (y<=sqrt(x) && y>=x^3){
compteur<-sum(compteur,1)
points(x,y,col='green',pch='•')# place dans le reperele point (x,y)
}
else (points(x,y,col='red',pch='-'))
}
aire<-compteur/nbsimul# estimation frequetiste de l'aire
text(x=0.5,y=0.5,paste(" estimation" ,round(aire,4),"\n taille",nbsimul),col=rgb(1,0,1),font=15,cex=0.8)
}
#----------------------------------- fin de la fonction----------------------------------------##---------programme principal -------------#for( n in c(100,250,500,1000))(MonteCarlo(n))