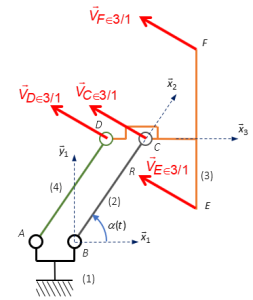
Champ des vecteurs vitesse d'un solide en translation à trajectoire circulaire
Exemple : Essuie-glace d'autobus
Considérons le mouvement de translation à trajectoire circulaire du balais 3 de l'essuie-glace par rapport au châssis 1 de l'autobus.
En tout point \(M\), \(\overrightarrow{V_{M\in3/1}}=\overrightarrow{V_{C\in3/1}}+\overrightarrow{MC} \wedge \overrightarrow{\Omega_{3/1}}=\overrightarrow{V_{C\in3/1}}\) car \(\overrightarrow{\Omega_{(3/1)}}=\vec{0}\).
Or, \(\overrightarrow{V_{(C\in3/1)}}=\overrightarrow{V_{(C\in2/1)}}\) car \(C\) est fixe dans 2 et dans 3.
Et \(\overrightarrow{V_{(C\in2/1)}}\) est perpendiculaire au rayon \(BC\) (voir partie « champ des vecteurs vitesse d'un solide en rotation »).
Fondamental : On retiendra les résultats suivants
Le vecteur vitesse angulaire est nul : \(\overrightarrow{\Omega_{3/1}}=\vec{0}\)
Tous les points, fixes dans le solide en translation circulaire, ont le même vecteur vitesse.