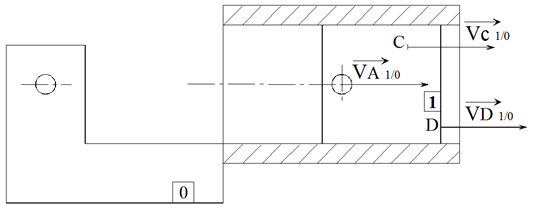
Champ des vecteurs vitesse d'un solide en translation à trajectoire rectiligne
Tous les points d'un solide en mouvement de translation ont la même vitesse (même direction, même sens et même intensité).
On dit que le champ des vitesses d'un mouvement de translation est uniforme.
La direction est parallèle à l'axe de translation de la liaison, glissière ou pivot glissant.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Exemple : Téléphérique
Considérons le mouvement de translation à trajectoire rectiligne de la cabine 2 par rapport à la station 1. Ce mouvement est de direction \(\vec{x_1}=\vec{x_2}\).
Pour tout point \(M_2\) fixe dans 2 \(\overrightarrow{V_{M_2\in2/1}}=\overrightarrow{V_{O_2\in2/1}}+\overrightarrow{M_2O_2} \wedge \overrightarrow{\Omega_{2/1}}=\overrightarrow{V_{(O_2\in2/1)}}\) car \(\overrightarrow{\Omega_{2/1}}=\vec{0}\).
Fondamental : On retiendra les résultats suivants
Le vecteur vitesse angulaire est nul : \(\overrightarrow{\Omega_{2/1}}=\vec{0}\)
Tous les points, fixes dans le solide en translation, ont le même vecteur vitesse ;
Ce champ des vecteurs vitesse est uniforme et colinéaire à la direction du mouvement ;
Ce vecteur vitesse, s'exprime sans calcul, à partir de la dérivée du paramètre de mouvement de la translation. Dans notre exemple, on a donc : \(\forall M\), \(\overrightarrow{V_{M\in2/1}}=\dot \lambda (t) \vec{x_1}= \frac{d\lambda(t)}{dt}\).
