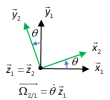
Champ des vecteurs vitesse d'un solide en rotation autour d'un axe fixe

Mouvement de rotation autour d'un axe fixe

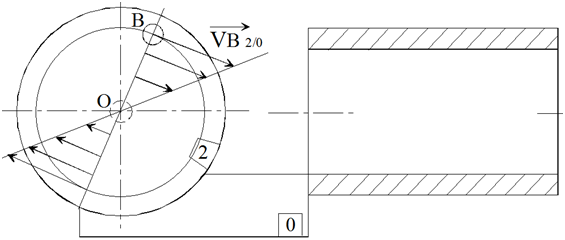
  • La direction de la vitesse d'un point est perpendiculaire au rayon entre le point et le centre de rotation.

  • Son intensité est proportionnelle au rayon entre le point et le centre de rotation, \(\|\overrightarrow{V_{(B\in2/0)}}\|=\|\overrightarrow{OB}\| \cdot \omega= R \cdot \omega\)

On dit que le champ des vitesses d'un mouvement de rotation est à caractéristique linéaire.

Si je connais la vitesse d'un point, j'en déduis la vitesse simplement la vitesse d'un autre point par une règle de proportionnalité.

Fondamental

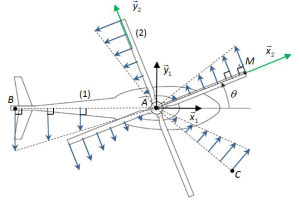
Considérons le mouvement de rotation d'axe \((A,\vec{z_1})\), paramétré par l'angle \(\theta(t)\), des pales 2 par rapport au fuselage 1 d'un hélicoptère.

  • Un mouvement de rotation a son axe immobile. Ainsi, en tout point \(I\) de l'axe de rotation \((A,\vec{z_1})\),la vitesse est nulle, \(\overrightarrow{V_{I\in2/1}}=\vec{0}\).

  • Le vecteur vitesse de tout point \(M\notin (A,\vec{z_1})\) est tangent à sa trajectoire en arc de cercle et donc perpendiculaire au rayon de cet arc de cercle, \(\overrightarrow{V_{I\in2/1}} \bot \overrightarrow{AM}\).

  • La norme du vecteur vitesse de tout point \(M\) est proportionnelle à la distance à l'axe de rotation et à la vitesse angulaire du mouvement en rad.s-1. Si \(M\) est à une distance R de l'axe \((A,\vec{z_1})\) alors \(\left \| \overrightarrow{V_{M \in 2/1}} \right \| =R \times |\dot\theta|\).