Pendule

Le pendule, qu’il soit étudié en pendule inverse ou en grue, est un système non-linéaire. Outre le fait que le système est soumis à des frottements et à des zones mortes, le mouvement lui-même est non-linéaire. Il faudra très probablement (et c’est une démarche tout à fait industrielle) linéariser le modèle autour de ses points de fonctionnement.

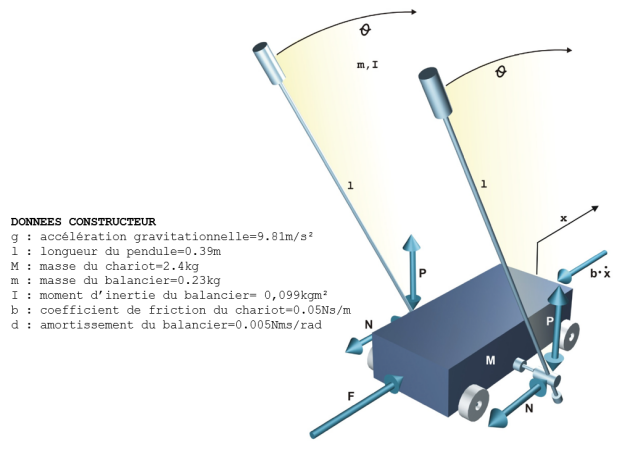
Sur la figure suivante, on pose les différentes grandeurs physiques caractéristiques du pendule. Les deux équations du mouvement fournies dans la documentation sont :

\((m+M)\ddot{x}+b \dot{x}+ml \ddot{\theta} \cos(\theta)-ml{\dot{\theta}}^2 \sin(\theta)=F\)

\((I+ml^2)\ddot{\theta}+mgl \sin(\theta)+ml \ddot{x} \cos(\theta)+d \dot{\theta}=0\)

Il ne s’agit pas ici de chercher à obtenir ces équations et nous verrons par la suite que ce n’est pas forcément utile pour l’élaboration d’un régulateur efficace. Nous accepterons donc telles quelles les équations données plus haut.

Par ailleurs, linéariser les équations consisterait à éliminer les fonctions trigonométriques en faisant l’hypothèse des petits angles ou en utilisant les développements de Taylor. La lourdeur de la démarche justifie pleinement que nous passions outre cette phase sans pour autant ignorer qu’elle est envisageable.

Les équations linéarisées, toujours fournies dans la documentation, sont :

\((m+M)\ddot{x}+b \dot{x}+ml \ddot{\theta} -ml{\dot{\theta}}^2 \theta=F\)

\((I+ml^2)\ddot{\theta}+mgl \theta+ml \ddot{x} +d \dot{\theta}=0\)