3.2. Régime libre
Le pendule (sans le chariot) est un système qui réagira librement à un stimulus de type « conditions initiales » (voir cours pages 21 à 23). C’est pour cela que l’on parle de « réponse libre » ou de « régime libre ». Mais on peut également soumettre le pendule à un stimulus désiré, c’est-à-dire une consigne (imposée par le chariot cette fois). On parle alors de « régime forcé ».
Dans un premier temps, on ne va s’intéresser qu’à la partie « balancier », c’est-à-dire en considérant le chariot fixe, donc en régime libre.
Préparation
Pendule simple non amorti : On considère un pendule simple, c’est-à-dire sans inertie. Par ailleurs, on néglige le coefficient d’amortissement au pivot. Ecrire les équations linéaires du mouvement du balancier dans le cas d’un pendule simple, c’est-à-dire l’équation différentielle qui donne l’angle q. Quelle est la valeur de la pulsation naturelle en régime libre ? Quelle est l’influence de la masse ? Est-ce normal ?
Préparation
Pendule simple amorti : On ajoute maintenant un coefficient d’amortissement au pivot du pendule. Réécrire les équations du mouvement. La pulsation naturelle a-t-elle changé ?
Attention :
Le coefficient d’amortissement donné dans le cours n’est pas tout à fait considéré de la même façon que dans notre cas pratique.
Nous avons fait l’hypothèse de petits angles sans quoi l’équation différentielle ne peut être résolue. Néanmoins, grâce à la représentation d’état, il est possible de tenir compte du terme en « sinus ».
Manipulation
Créer un fichier Simulink qui regroupe les modèles
du pendule simple sans la non-linéarité en sinus
du pendule simple amorti sans la non-linéarité en sinus
du pendule simple avec la non-linéarité en sinus
du pendule simple amorti avec la non-linéarité en sinus
et simuler les modèles en utilisant la représentation d’état. On prendra les valeurs données un peu plus haut. Comparer le comportement des modèles et mesurer leurs pulsations naturelles.
Remarque :
Tout au long du TP, on utilisera le fichier fft_teta.m pour mesurer les pulsations naturelles. Attention !! : Le résultat est donné en Hz et non en rad/s!! Afin de pouvoir utiliser la fonction fft_teta, il est obligatoire de faire une sauvegarde des données sur l’espace de travail avec le bloc simulink « to workspace » disponible dans la catégorie « sinks » de simulink.
Le modèle utilisant le sinus et l’amortissement est forcément plus précis. On gardera donc cette description, pour l’instant en tout cas.
Préparation
On considère maintenant un pendule dit « pendule lourd » ou « pendule pesant » ou encore « pendule physique ». Il sera donc maintenant doté d’une inertie. Que devient l’équation du mouvement ? Retrouve-t-on les équations mentionnées en introduction ? Quelles conclusions en tirer ?
Remarque :
Les équations du pendule pesant ne sont volontairement pas données. Deux solutions s’offrent à l’étudiant brillant :
il connait parfaitement la physique et déduit les équations du système
il sait utiliser la recherche d’informations sur internet et surtout faire le tri de tout ce qu’il va trouver.
Dans les deux cas, il s’agit ici d’autonomiser la recherche. Il est également possible de la faire à plusieurs, voire plusieurs groupes.
Manipulation
Créer un fichier Simulink qui regroupe les modèles
du pendule simple amorti avec la non-linéarité en sinus
du pendule lourd amorti avec la non-linéarité en sinus
et simuler les modèles. Mesurer les pulsations naturelles. Conclure.
Il s’agit maintenant de comparer les résultats de simulation avec la réalité.
Manipulation 
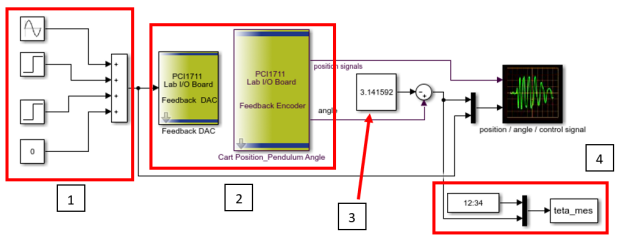
On sollicitera manuellement le balancier avec un petit angle (le chariot ne doit pas bouger pendant le balancement). Le fichier RT_identif.slx permet de faire une acquisition de données. Avant de lancer la manipulation, l’enseignant doit vérifier.
1 – Etage d’entrée ; 2 – Système ; 3 – Compensation d’offset (référence constructeur q=0 lorsque le pendule est vertical) ; 4 – Sauvegarde de la simulation dans l’espace MatLab.
Préparation
La valeur du moment d’inertie donnée par la documentation semble erronée. Est-ce réellement le cas ? Quelle procédure devrait-on effectuer afin d’en obtenir la vraie valeur ?
Manipulation 
Mettre en place le protocole d’identification/mesure du moment d’inertie en utilisant le fichier RT_identif.slx . Avant de lancer la manipulation, l’enseignant doit vérifier.
Manipulation 
Mesurer la pulsation naturelle du pendule réel. Essayer d’identifier le coefficient d’amortissement. La différence avec le modèle est-elle significative ?
Manipulation 
Après avoir opéré un recalage des paramètres des modèles, lancer une simulation sous Simulink mettant en parallèle le modèle élaboré pour le pendule simple et pour le pendule pesant (modifier le fichier RT_identif.slx et le sauvegarder sous un nom différent). Quelles conclusions peut-on en tirer ? Quelle est la différence majeure ? Peut-on valider le modèle ? Comment recaler les paramètres ?