3.5. Modèle complet
On dispose maintenant d’un modèle du balancier et d’une valeur de zone morte du chariot. Il manque un modèle dynamique du chariot. Il est évident que le mouvement du balancier va influer sur la position du chariot par inertie. Il faudra donc considérer le balancier comme une « perturbation » du système « chariot ».
Le chariot est un système très fortement non-linéaire. La manipulation suivante va le démontrer.
Manipulation 
Prendre le fichier RT_identif.slx. Faire une sauvegarde de la position du chariot dans l’espace de travail (sauvegarder le temps, l’échelon et la position). Stimuler le chariot avec un échelon de 0,15m démarrant à une seconde. Limiter l’essai à 5 secondes au total. Faire l’essai 3 ou 4 fois en partant toujours de la position centrale, balancier au repos. (Utiliser la fonction plot puis faire « hold ». Superposer les courbes obtenues) Que constatez-vous ? Que pouvons-nous conclure ?
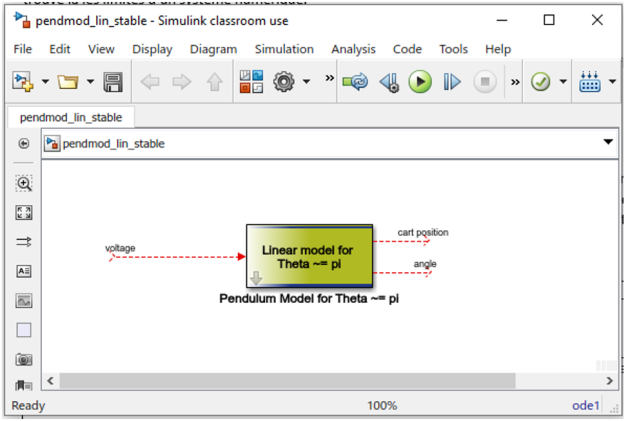
Le constructeur donne un modèle complet linéaire du système (fichier pendmod_lin_stable.slx).
Manipulation 
Prendre le fichier RT_identif.slx. Insérer le modèle linéaire fourni par le constructeur et le faire tourner en parallèle du système réel sur une simulation de quelques secondes avec un échelon de 0,15 en entrée. Quelles conclusions peut-on en tirer ?
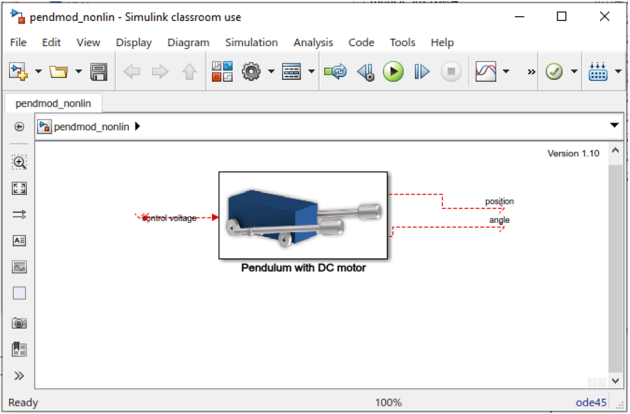
Le constructeur fourni un autre modèle, visiblement bien plus complet et surtout fortement non-linéaire (fichier pendmod_nonlin.slx)
Manipulation 
Prendre le fichier RT_identif.slx. Insérer le modèle non-linéaire fourni par le constructeur et le faire tourner en parallèle du système réel sur une simulation de quelques secondes avec un échelon de 0,15 en entrée. Quelles conclusions peut-on en tirer ?
L’étudiant curieux ouvrira quelques blocs du modèle non-linéaire fourni afin de se rendre compte de la difficulté de la modélisation non-linéaire.